Computational Intelligence Robotics Laboratory
The Computational Intelligence Robotics Laboratory (CIRL) is housed in the Department of Computing Sciences in the Science Faculty of the Nelson Mandela Metropolitan University in Port Elizabeth, South Africa. CIRL conducts research on the application of Computational Intelligence techniques to robot control and design, with a special focus on Evolutionary Robotics.

Evolutionary Robotics
Evolutionary Robotics (ER) is a sub-field of Evolutionary Algorithms which comprises of optimisation algorithms inspired by biological evolution. These are stochastic algorithms which employ a population of potential solutions which is iteratively improved by allowing better performing solutions to act as parents to future generations. Good characteristics are thus kept in the population with the aim of locating the global optimum in the search space.
ER can be used to evolve robot morphologies and controllers. Although some work has been done within CIRL in the field of evolving both the morphology and controller of robots [1], most of the current work is focussing on evolving controllers only. A controller is the program that determines robot behaviour. An open-loop controller is a sequence of movements that will allow a robot to perform a task. A closed-loop controller makes use of sensory input to judge the robot's state, so that each movement command is in response to the state of the robot and the progress in performing its task. A basic ER algorithm is given below:
-
Randomly create a population of controllers
-
While no satisfactory solution is found
-
Evaluate the performance of all population members
-
Select individuals to act as parents (favouring the better performing individuals)
-
Create offspring individuals by performing crossovers and mutations on parents
-
Replace the main population with the offspring population
A drawback of using the ER approach is the large number of performance evaluations that must be performed. A population of 100 individuals which is evolved for 10000 generations would require about 1000000 controller evaluations on the robot. This may lead to wear and other damage to the robot, especially as some controllers may result in movements that may mechanically injure the robot. Furthermore, evaluating the performance of the controllers on the robot can be extremely time consuming.
Simulation in Evolutionary Robotics
The evaluation of large numbers of controllers in the real world during the ER process is generally not feasible. Researchers typically make use of physics simulators so that evaluations can be performed in software. Controllers can be evolved in simulation and then be transferred to the real world when an adequate solution is found. A major stumbling block of this approach is what is referred to in literature as the reality gap. The reality gap problem is caused by differences between simulated and real world behaviour. The ER process often exploits these differences to evolve controllers that perform well in simulation, but that do not transfer well to reality.
The traditional technique of creating simulators is to calculate robot movements based on kinetic and mechanical laws. Unfortunately, it is almost always necessary to make simplifying assumptions about the robot and the environment. This leads to inaccuracies which quickly compound to result in poor simulation performance which leads to the reality gap problem. A further disadvantage of the traditional techniques is that the models are computationally expensive to simulate. Models may in some cases be so complex that they cannot be simulated in real time, thus resulting in ER evaluations that take longer than what it would have taken to evaluate the controllers in the real world.
Neural Networks as Simulators
One of the main focus areas of CIRL is the hypothesis that Neural Networks (NNs) can be utilized to act as simulators in the ER process. A NN is a model of the biological brain which consists of interconnected computational units called neurons. NNs can be trained through a process called supervised learning to learn to produce a desired output based on a given input. With regards to acting as a simulator for a robot, a NN must be trained to predict the position and state of a robot as a result of a command, based on the current position and state. The robot can then be simulated by iteratively presenting the NN with a command and then feeding the outputs (the state and position) to the NN with the next command. Note that NNs can also be trained to simulate sensors that may be attached to the robot.
We believe that using NNs as simulators in the ER process is beneficial because:
-
NNs are comparatively computationally inexpensive to execute,
-
little or no understanding of the underlying physics is required by the experimenter, and
-
the NN simulator can be trained using data from the actual robot it is to simulate, thus robot-specific idiosyncrasies are automatically taken into account.
The following methodology was thus proposed to create a NN simulator for a robot:
-
Issue random commands to the robot.
-
Track the displacement and state change of the robot after each command.
-
Record the sensor readings of the robot after each command.
-
Repeat steps 1, 2 and 3 until sufficient data is obtained.
-
Parse the data into training patterns consisting of inputs (command, state and sensor readings) along with expected outputs (displacement, new state and new sensor readings).
-
Train a NN on the training patterns using an appropriate training algorithm.
After the NN is trained, it can be used in the ER process to simulate the behaviour of the robot.
Proof of Concept
The previous section highlighted the hypothesis that NNs can be used as simulators in the ER process. The CIRL research group has made significant progress in proving this hypothesis by means of several proof of concept experiments. A very brief overview of these experiments is given here. The interested reader is encouraged to read the relevant papers that are referenced with each experiment.
Our first investigation involved the creation of a motion simulator for a simple differentially steered Lego robot [2]. The simulator was created using the methodology described in the previous section. Here no sensors were present and all data could be gathered by filming the robot and then parsing the change in position and orientation of the robot from the video. The NN was trained to predict the position and orientation changes of the robot based on the following inputs: the current motor commands, the previous motor commands, and the duration that the commands were maintained. The simulator was used in the ER process to evolve a controller to perform a simple task. The controller consisted of a sequence of motor commands and the goal was to manoeuvre the robot through a sequence of blocks on the operating surface and return to the starting block. A constraint was introduced that the robot was not allowed to leave the operating surface or enter a forbidden area in the centre of the operating surface. The ER process managed to evolve a suitable controller in simulation. This controller transferred well when executed on the real world robot (refer to Figure 1). A video of the robot is available below. This experiment thus demonstrated that it is possible to successfully use NN simulators in the ER process.
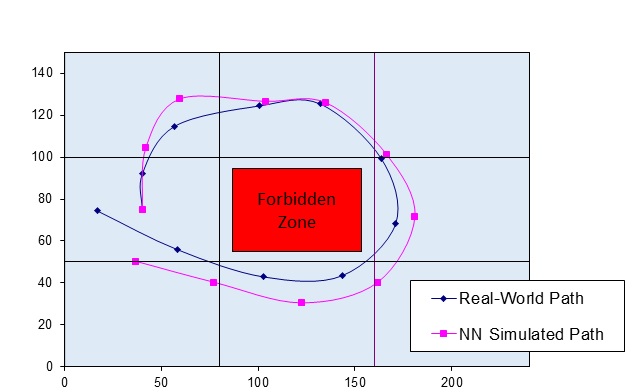
Figure 1
The next phase of investigation involved the incorporation of sensors into the simulator. A NN was trained to simulate the functioning of a light sensor [3]. A light source was introduced onto the robot’s working surface and the robot was equipped with two forward-facing light sensors. Random motor commands were issued and the light sensor readings at various locations were recorded. The light simulator NN thus took as input the robot’s distance from the light source and relative orientation and then was expected to output the difference in sensor values between the two light sensors and the average sensor value of the sensors. The motion simulator was also adapted so that it predicts the movements after a constant amount of time (400ms). The duration of the commands was thus removed as input to the NN. The trained NN simulators were used in the ER process to evolve a NN controller for the robot. The aim of the controller was to move the robot towards the light source from any location on the working surface. A successful controller was evolved, demonstrating that a NN can be used as a simulator for a light sensor in the ER process. Figure 2 shows the simulated and real world paths followed by the robot when controlled by the evolved NN controller. The figure shows how the robot moves towards the light source from five different starting positions. Note that excellent correspondence was found between simulated and real world behaviour.
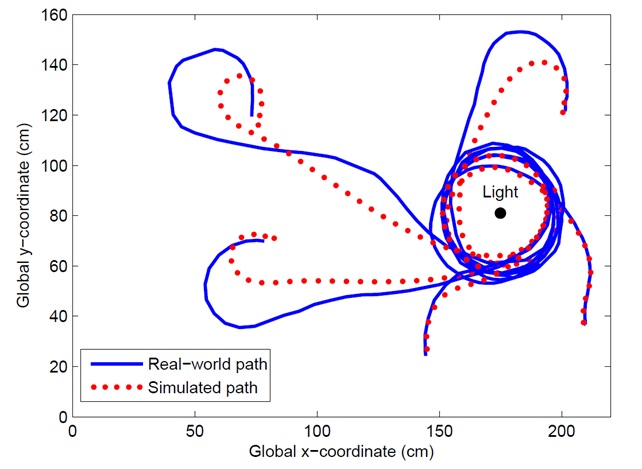
Figure 2
The natural next step in the research involved the incorporation of more sensors [4,5]. Two additional sensors were modelled using a NN: an ultrasonic distance sensor and a touch sensor. Once again, no physics models were used in creating these simulators. The NN was trained only on data obtained by issuing random commands to the robot. Modelling the ultrasonic sensor was a challenge, as it is generally very inaccurate, resulting in large amounts of noise in the training data. However, the NNs were successfully trained to act as simulators for both sensors. These simulators were used in the ER process to evolve controllers for the robot. An obstacle avoidance task was setup for the robot, whereby it had to traverse from a start position to a target position without being trapped by the obstacles present on the working surface. Each controller consisted of a sequence of motor commands. Each of the commands would be executed until an input from the sensors is received. Controllers were successfully evolved using each of the sensors. The evolved controllers transferred correctly to the real world robot environment. Figure 3 shows the simulated and actual paths of the robot for the controller that made use of the touch sensor. It should be noted that the four paths shown in the figure represent four different controllers.
The encouraging results on the differentially steered robot demonstrated that NN simulators could indeed be used in the ER process. However, the technique had only been demonstrated on a very simple robot. The generalisability to a more complex robot needed to be demonstrated. As such NN simulators were employed in evolving a controller for a balancing robot (refer to Figure 4) [5]. This robot consists of two wheels independently controlled by motors. A gyroscopic sensor and accelerometer sensor are present to detect movement and tilt of the robot. The goal of this robot is to balance by moving the wheels forward and backwards, given inputs from the sensors (this is also referred to as the inverted pendulum problem in the literature).
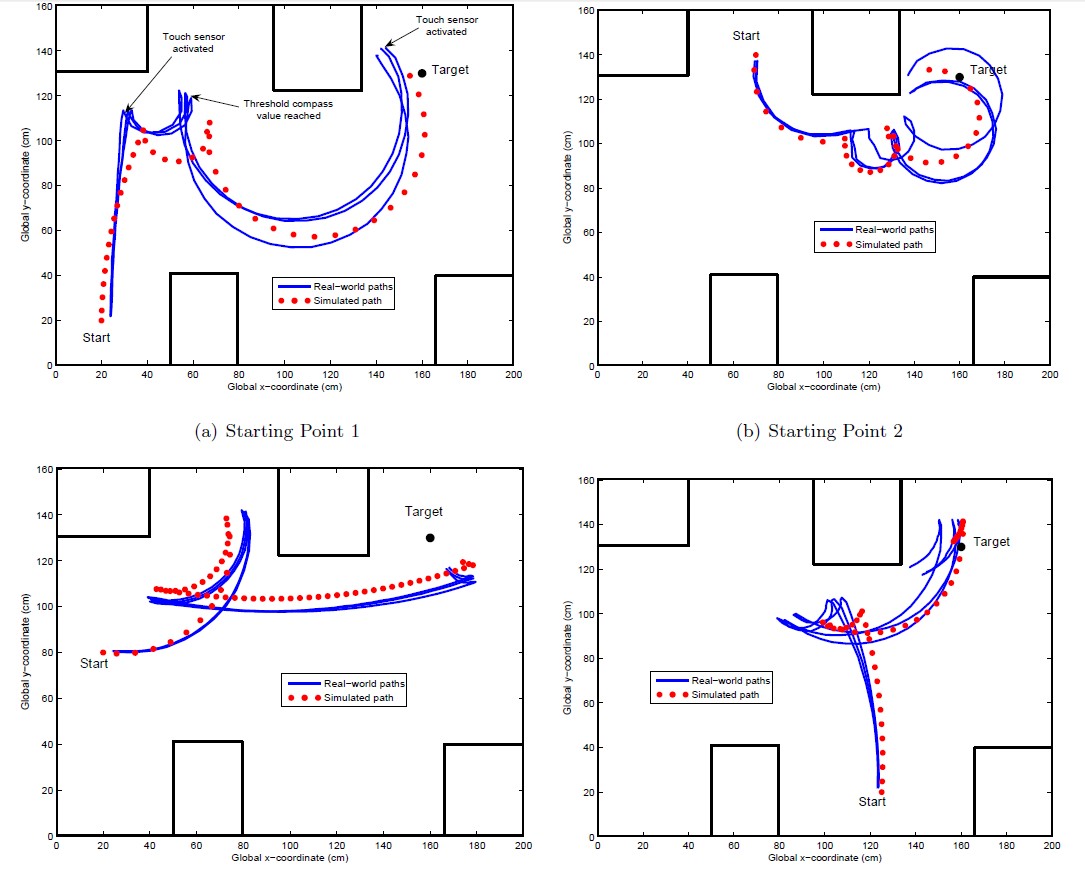
Figure 3

Figure 4
A simulator that can model the robot’s change in state, in response to a motor command was needed before ER could be used to evolve a controller. This NN simulator takes as input the previous motor commands, the current motor commands, the current tilt sensor value and the current gyroscopic sensor value. The outputs of the NN is the new tilt and gyroscopic sensor values. Using this NN simulator, a controller could be evolved that issues motor commands that minimises change in tilt and gyroscopic value (i.e. keeps the robot as steady as possible while standing upright).
A slightly different data acquisition methodology had to be followed with the balancing robot, as the process was not as simple as just issuing random commands as was the case with the differentially steered robot. The balancing robot would fall over after virtually any random command. To solve this problem, two support bars were added to the robot during the data acquisition phase. This prevented the robot from falling over as random commands were executed. The obtained training data was pre-processed to remove all instances where the robot was tilted more than a few degrees (i.e. where the support bars would touch the ground), thus leaving only patterns where the robot was within balancing range. Once again, noise was present due to inaccuracies of the sensors. The noise problem was compounded by the fact that controller commands must be issued frequently, thus requiring the simulator to predict sensor values every 12ms. Despite these challenges, simulator NNs were successfully trained and used in the ER process to evolve a balancing controller. A video of the balancing robot can be viewed here []. This experiment proved that NN simulators can be used even for challenging robotic tasks.
Further investigations into the use of NN simulators in the ER process for more complex robots are underway. A NN simulator was used in conjunction with an existing locomotion model for a snake robot to evolve a controller and let the snake visit specific positions of the working surface [6]. The locomotion model makes use of wave functions to make the snake slither at different speeds in different directions based on the parameters supplied to the model. A NN was trained to predict the displacement and change in orientation of the robot for a given parameter set. The NN was successfully used in the ER process to evolve a sequence of parameters which, when used in the locomotion model, allows the snake to move to the required positions on the working surface (refer to the paths shown in Figure 5).
Figure 5
Neural Network vs Traditional Simulators
The experiments described in the previous section showed that it is indeed possible to use NN simulators in the ER process. The logical next question is: Which is better, a NN simulator or a traditional physics-based simulator? NN simulators have the obvious benefit that very little expert knowledge and insight are needed for their creation. However, this benefit would not be very useful if the NN simulators take much longer than traditional simulators to execute, or if the evolved controllers do not transfer well to the real world due to inaccuracies in the simulator. Research is required to determine which type of simulator is superior.
The first comparison between NN and physics simulators for use in ER was conducted on a simple differentially steered robot (a Khepera III robot was used) [7]. Two physics models were used for the comparison. The first is a basic kinematics model which makes several simplifying assumptions for the sake of computational efficiency (for example, inertia and momentum were ignored). The second is a much more comprehensive dynamics model in which the robot is described by means of five first-order coupled differential equations. A numeric integrator was used to derive simulation predictions from this model.
The three simulators were utilised in the ER process to evolve controllers for the robot to enable it to visit a sequence of positions on the working surface. Experiments were repeated 30 times to see how successful each of the approaches are in general. The results showed that the simple kinematic simulator was slightly faster to execute than the NN simulator, but that both were much faster than the dynamics model. In terms of transferability, however, it was found that the NN simulator performed best: firstly in terms of having the most number of controllers that transferred correctly to the real world, and secondly by having the smallest actual difference between the simulated and real world behaviour in terms of the fitness function. The kinematics model produced the most inaccurate controllers. The results found in these experiments are very encouraging as it demonstrated the superiority of the NN simulator over the dynamics simulator both in terms of accuracy and time, and was shown to be significantly more accurate than the kinematics simulator. Although the kinematic model proved to be faster than the NN simulator, the controllers it produced were of a very low quality. It can thus be concluded that in this case it would be best to use a NN simulator.
The encouraging results found for the Khepera robot prompted the extension of the comparison to the more complex balancing robot [8]. Once again two physics simulators were compared to the NN simulator. A linear and a non-linear physics model were used. Although the linear model is computationally much simpler than the non-linear model (it makes several simplifying assumptions about the robot), both models are quite complex and have several parameters that are difficult to estimate. These parameters were optimised using a GA and data collected from issuing random commands to the robot (the training data for the NN), in order to give the physics simulators the benefit of the doubt. Despite the attempts at optimising the physics simulators and various investigations into introducing an appropriate amount of noise into the physics simulations, the controllers that were evolved using the physics models transferred poorly to the real world. Out of all the experiments that were conducted, only one controller actually managed to balance the robot in the real world. In contrast, the controllers evolved using the NN simulators performed much better when executed on the real robot. The results of this investigation showed that for a complex robot, NN simulators was the only viable simulation technique in the ER process as the reality gap was drastically narrowed.
Bootstrapping Neural Network Simulators
The use of NN simulators as described so far involves first collecting data from the robot, then training the NN simulator and afterwards using the trained simulator in the ER process. However, it was hypothesised that the simulator training process could be incorporated in the ER process, thus saving valuable time. The proposed technique is summarised in the algorithm below:
-
Initialise a NN with random weights to act as a simulator
-
Create a population of random controllers
-
While a suitable controller has not been found
-
Evaluate one of the controllers on the real world robot
-
Concurrently train the NN simulator (if training patterns are available)
-
Concurrently execute the ER process using the NN simulator
-
Add the real world evaluation to the training set of the simulator
The above approach collects training data for the NN simulator while the ER process is underway. As the simulator becomes more accurate, the ER process finds better controllers. These controllers are evaluated in the real world, thus creating more training data for the simulators. The key benefit of using this approach is that the NN simulator is trained on patterns that relates directly to the controller that is being evolved. It is thus not necessary to create a general simulator which can simulate any controller, thus reducing the number of real world evaluations that must be performed. The approach is very elegant in the sense that the robot starts with no information on how it functions and gradually builds up a model of itself which it uses to learn a way to perform a desired task. The simulator is thus bootstrapped during the ER process and the approach is referred to as Bootstrapped Neuro-Simulation.
The first experiments investigating the bootstrapping approach focused on evolving controllers for the Khepera robot [9]. Once again the goal was to evolve a sequence of motor commands which would make the robot visit a desired list of points on the working surface. However, in this case the NN simulator was not trained before the ER process but during the evolution. Training data was obtained by periodically evaluating controllers in the real world. Figure 6 shows how the fitness of the controller in the real world compares to the fitness in simulation. Initially, the simulator is very poor and only a poor solution can be evolved. However, as the simulator improves the simulated fitness becomes better as more effective controllers evolve. Although the improved simulators are a result of better controllers, the correspondence between the simulated and real world environment takes a while longer to improve to the point where the difference between the simulated and real world fitness becomes small enough for the task to be successfully performed in the real world.
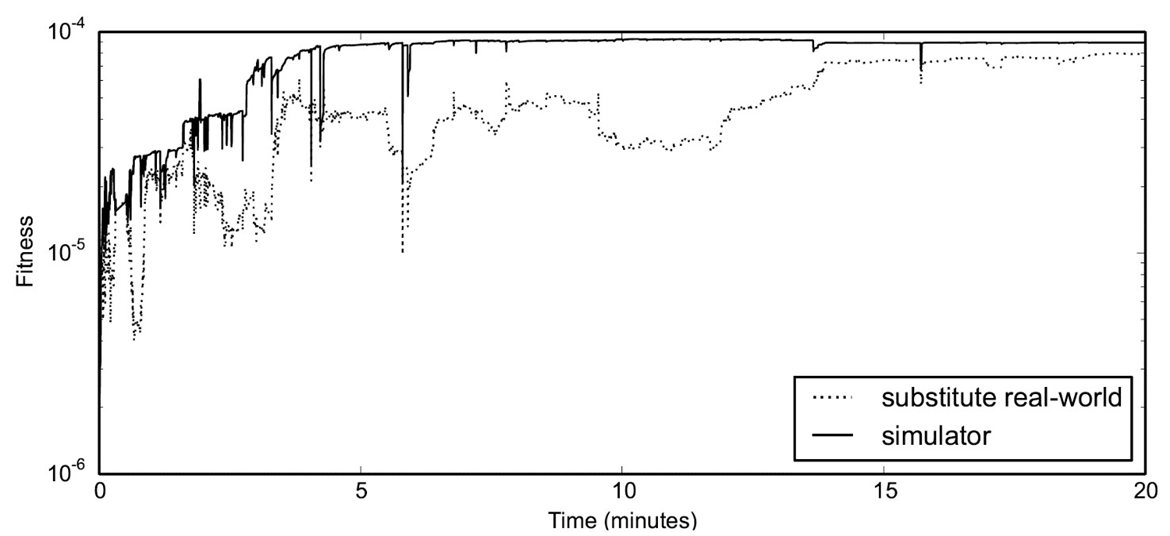
Figure 6
Successful controllers were evolved using the Bootstrapped Neuro-Simulation approach. Figure 7 shows a simulated and real world path that was evolved after 30 real world evaluations. The robot managed to build a model of itself and used that model to evolve a controller to traverse the seven required points in order, all in less than 30 minutes.
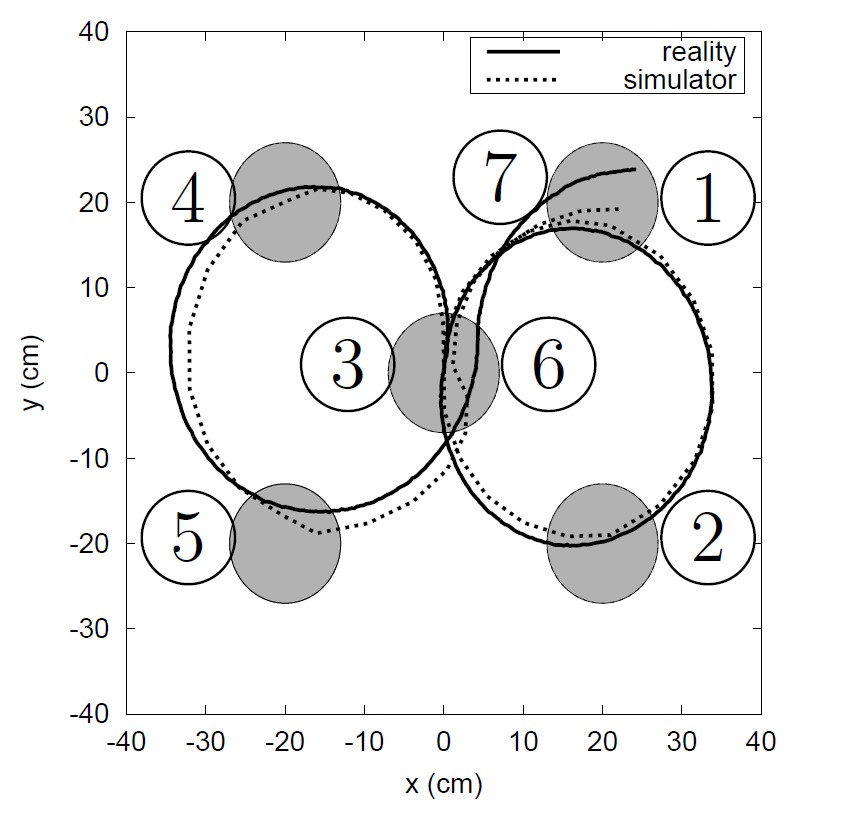
Figure 7
The Bootstrapped Neuro-Simulation approach was further validated by means of a snake robot [10]. Using a similar methodology as in [6], a locomotion model was to be parameterised by the ER process to let the snake visit specified regions on the working surface in order. The NN simulator had to learn how the locomotion model behaves for different sets of parameters. The solution shown in Figure 8 was obtained after only 46 real world evaluations. This is an extremely encouraging result considering the complexity of the robot and task. A video of the Bootstrapped Neuro-Simulation approach applied to the Khepera and snake robots is available below.
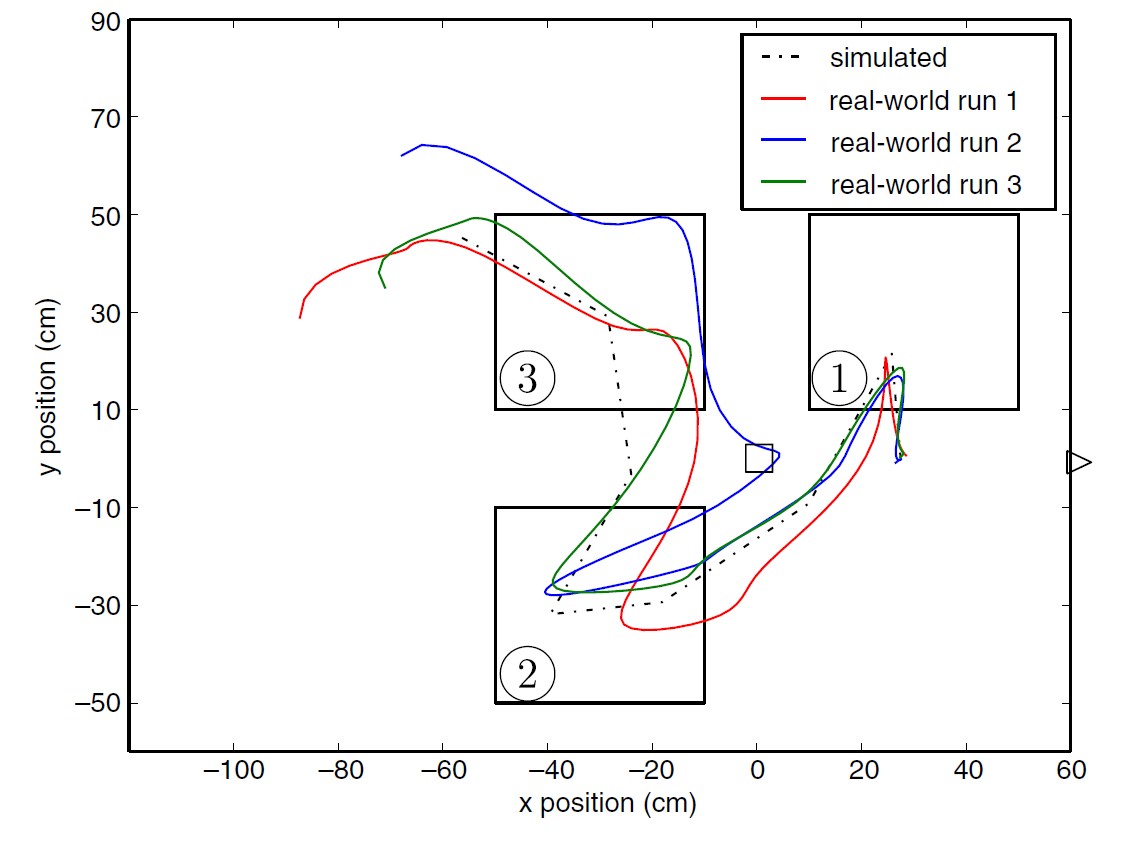
Figure 8
Staff
Dr Mathys C.du Plessis (mc.duplessis@mandela.ac.za)
Mr Christiaan J. Pretorius (christiaan.pretorius2@mandela.ac.za)
Prof Jean H. Greyling (jean.greyling@mandela.ac.za)
Students
Grant W. Woodford
Michael W. Louwrens
Waldo Scheun
Publications
1. Louwrens, M.W., du Plessis, M.C. and Greyling, J.H., 2016.
Using Standard Components in Evolutionary Robotics to Produce an Inexpensive Robot Arm. In Advances in Nature and Biological Inspired. Computing (pp. 128-139). Spring Interanational Publishing.
2. Pretorius, C.J., du Plessis, M.C. and Cilliers, C.B., 2009, October.
Towards an artificial neural network-based simulator for behavioural evolution in evolutionary robotics. In Proceedings of the 2009 Annual Research Conference of the South African Institute of Computing Scientists and Information Technologists (pp. 170-178). ACM.
3. Pretorius, C.J., du Plessis, M.C. and Cilliers, C.B., 2010, July.
A Neural Network- based kinematic and light-perception simulator for simple robotic evolution. In IEEE Congress on Evolutionary Computation (INFOCOMP'12), Venice, Italy.
4. Pretorius, C.W., du Plessis, M.C. and Cilliers, C.B., 2010, July.
A Neural Network Ultrasonic Sensor Simulator for Evolutionary Robotics, Proceedings of the Interantional Conference on Advanced Communitications and Computation (INFOCOM'12), Venice, Italy.
5. Woodford, G.J., du Plessis, M.C. and Cilliers, C.B., 2010, July.
Simulating robots without conventional physics: A neural network apporach. Journal of Intelligent & Robotic Systems, 71 (3-4),pp. 319-348. Spinger.
6. Pretorius, C.J., Du Plessis, M.C. and Cilliers, C.B., 2015, December.
Evolving Snake Robot Controllers Using Artificial Neural Networks as an Alternative to a Physics-Based Simulator. In Computational Intelligence. 2015 IEEE Symposium Series on (pp.267-274). IEEE. Cape Town, SA.
7. Pretorius, C.J., du Plessis, M.C. and Gonsalves, J.W., 2014, July.
A comparison of neural networks and physics models as motion simulators for simple robotic evolution. In 2014 IEEE Congress on Evolutionary Computation (CEC) (pp.2793-2800). IEEE. Beijing, China.
8. Pretorius, C.J., du Plessis, M.C. and Gonsalves, J.W., 2017.
Neuroevolution of inverted Pendulum Control: a Comparative Study of Simulation Techniques. Journal of Intelligent & Robotic Systems. Springer.
9. Woodford, G.W., Pretorius, C.J. and du Plessis, M.C., 2016.
Concurrent controller and Simulator Neural Network developement for a differentially-steered robot in Evolutionary Robotics. Robotics and Autonomous Systems, 76, pp.80-92.
10. Woodford, G.W., du Plessis, M.C. and Pretorius, C.J,. 2017.
Concurrent controller and Simulator Neural Network developement for a snake-like robot in Evolutionary Robotics. Robotics and Autonomous Systems, 88, pp.37-50.